The DeFi space is constantly changing and evolving.
Each time new ideas are presented on how to approach strategies to maximize profits.

As in any economy, balance is critical.

Here we present another way of understanding the so-called DeFi 1.0 introduced years ago by great projects such as Goose, Panther, and others.

Game Theory Background

Game theory is the study of mathematical models of strategic interactions among rational agents. It’s based on hard math, and its being studied since the early 1900.

Different criterias rises by the studies of John von Neumann and John Nash equilibrium. Where strategies for “non-cooperative” games involving two or more player are presented. This way, balanced strategies for equilibrium earnings are presented.

From here, the prisoner’s dilemma was presented.

The Prisoner’s dilemma

The prisoner’s dilemma is a standard example of a game analyzed in game theory that shows why two completely rational individuals might not cooperate, even if it appears that it is in their best interests to do so.

Two prisoners are separated into individual rooms and cannot communicate with each other. The normal game is shown below:

https://en.wikipedia.org/wiki/Prisoner%27s_dilemma

It is assumed that both prisoners understand the nature of the game, have no loyalty to each other, and will have no opportunity for retribution or reward outside the game. Regardless of what the other decides, each prisoner gets a higher reward by betraying the other (“defecting”). T

he reasoning involves analyzing both players’ best responses: B will either cooperate or defect. If B cooperates, A should defect, because going free is better than serving 1 year.

If B defects, A should also defect, because serving 2 years is better than serving 3. So either way, A should defect since defecting is A’s best response regardless of B’s strategy. Parallel reasoning will show that B should defect.

Because defection always results in a better payoff than cooperation regardless of the other player’s choice, it is a strictly dominant strategy for both A and B.

Mutual defection is the only strong Nash equilibrium in the game (i.e. the only outcome from which each player could only do worse by unilaterally changing strategy).

The dilemma, then, is that mutual cooperation yields a better outcome than mutual defection but is not the rational outcome because the choice to cooperate, from a self-interested perspective, is irrational.

Thus, Prisoner’s dilemma is a game where the Nash equilibrium is not Pareto efficient.

Game Theory Applied in DeFi 1.0

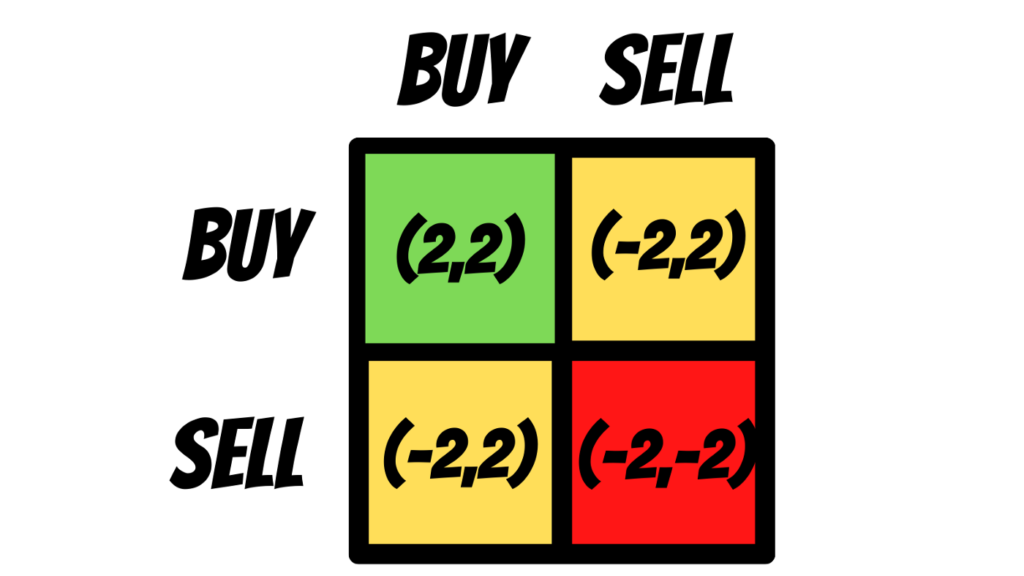
By thinking on the theory above and what OlympusDAO is proposing, we can have a specific matrix for DeFi 1.0.

The simplest model has two players with two possible actions:

Stake (Buy). Players are most likely to stake when they anticipate an expansion in supply and/or price. It has the effect of pushing the price up +2.
Sell. Players are most likely to sell when they anticipate a contraction in supply and/or price. Selling has the effect of pushing the price down -2.